Publications
Rethinking Graph Super-resolution: Dual Frameworks for Topological Fidelity
Pragya Singh and Islem Rekik
ArXiv
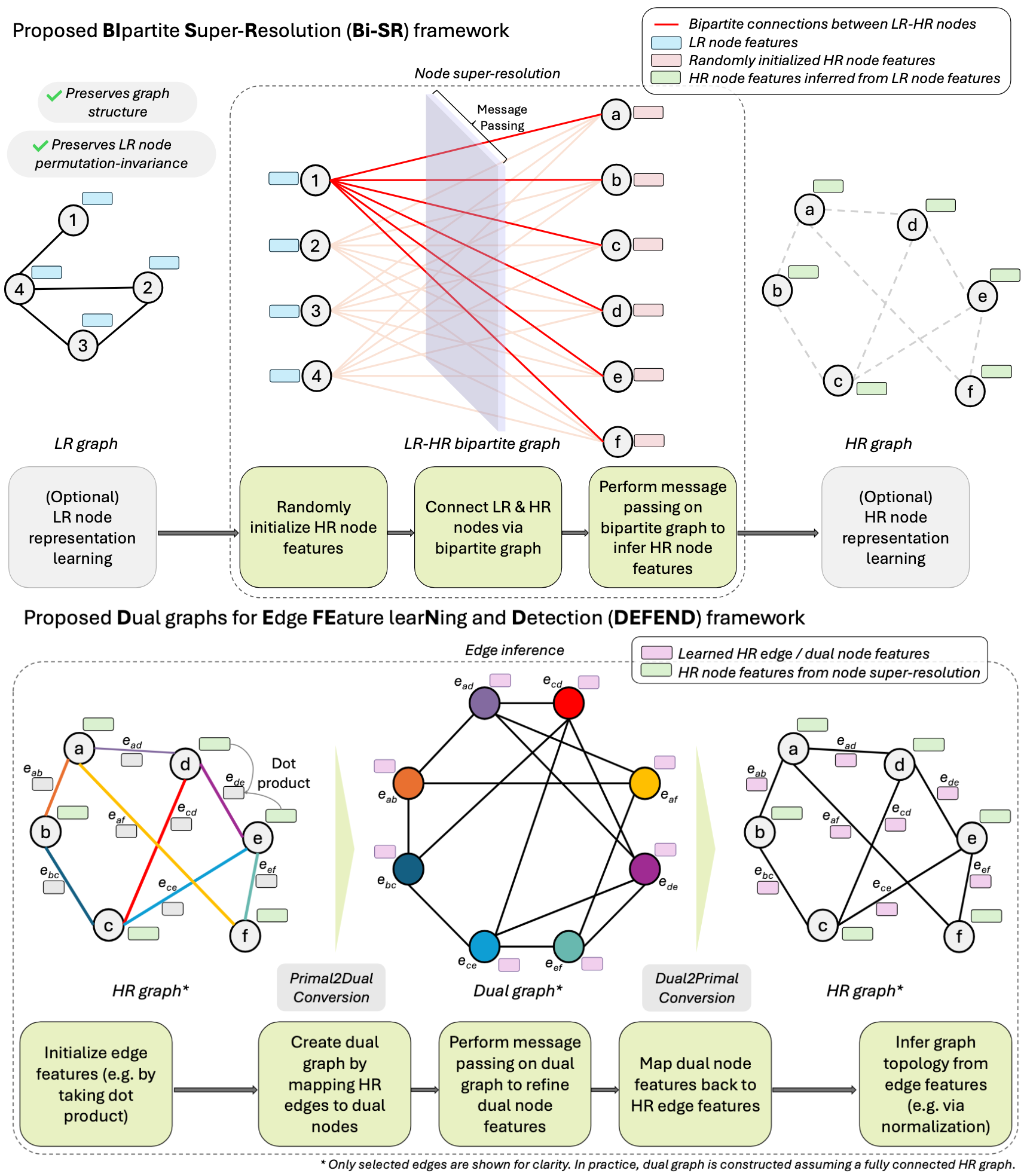
This work introduces two GNN-agnostic frameworks designed to overcome structural limitations in Graph Super-resolution (GSR). Bi-SR employs a bipartite graph for structure-aware, permutation-invariant node inference. DEFEND maps high-resolution (HR) edges to nodes in a dual graph, enabling efficient and expressive edge inference using standard GNNs. Both frameworks achieved state-of-the-art performance on a real-world brain connectome dataset and twelve new simulated datasets that capture diverse graph topologies and LR-HR relationships.
Strongly Topology-preserving GNNs for Brain Graph Super-resolution
Pragya Singh and Islem Rekik
PRIME-MICCAI 2024
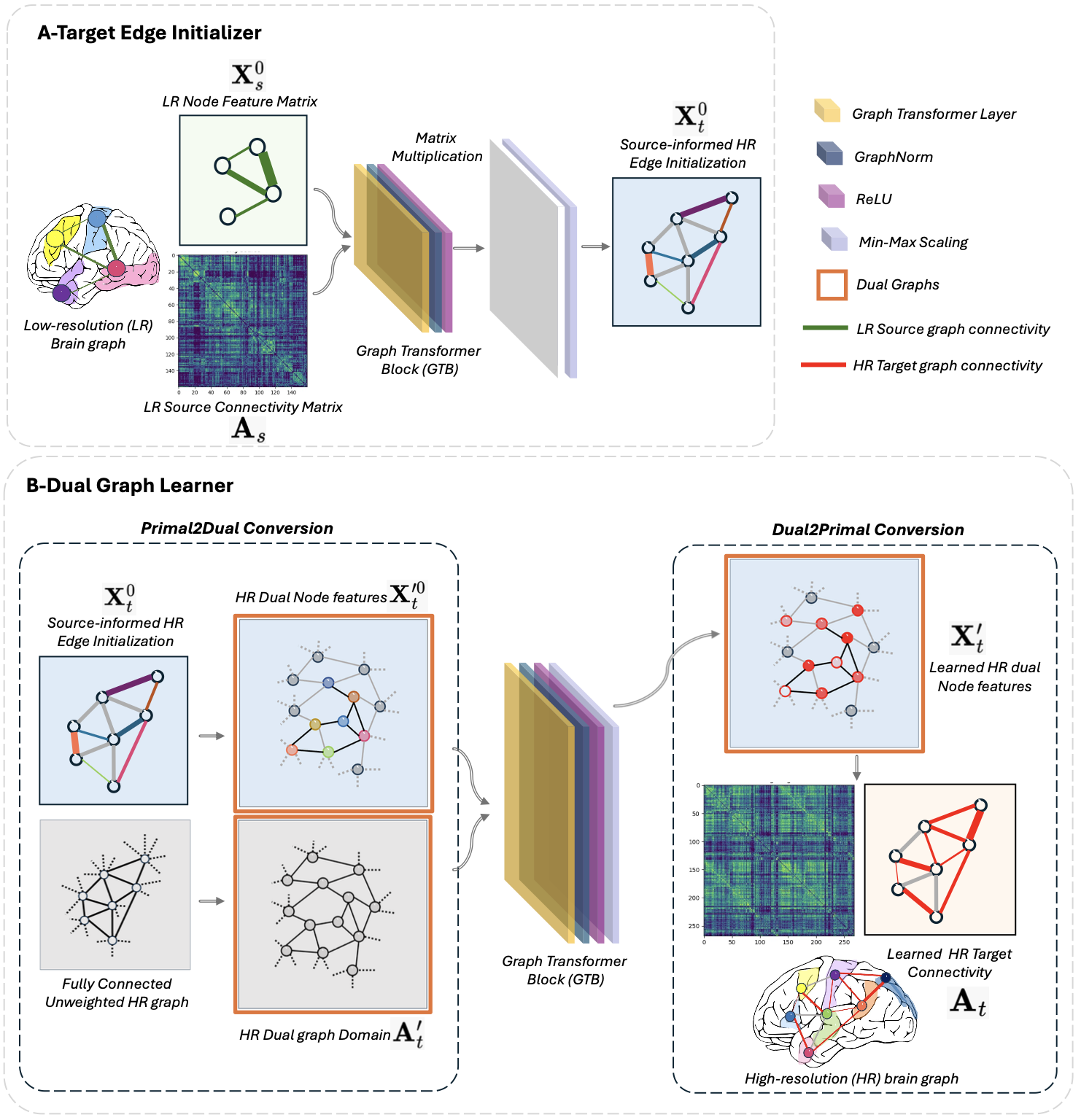
The Strongly Topology-Preserving GNN framework (STP-GSR) is the first graph super-resolution (GSR) architecture designed for direct edge representation learning. It addresses the computational demands and topological limitations of traditional node-based GNNs, which fail to capture crucial higher-order brain structures. STP-GSR leverages the primal-dual graph formulation to efficiently map the low-resolution (LR) edge space to the node space of a highly sparse high-resolution (HR) dual graph. This approach enforces strong topological consistency. Comprehensive benchmarking confirms STP-GSR significantly outperforms state-of-the-art methods across seven key topological measures
Group-invariant machine learning on the Kreuzer-Skarke dataset
Christian Ewert, Sumner Magruder, Vera Maiboroda, Yueyang Shen, Pragya Singh, Daniel Platt
Physics Letters B
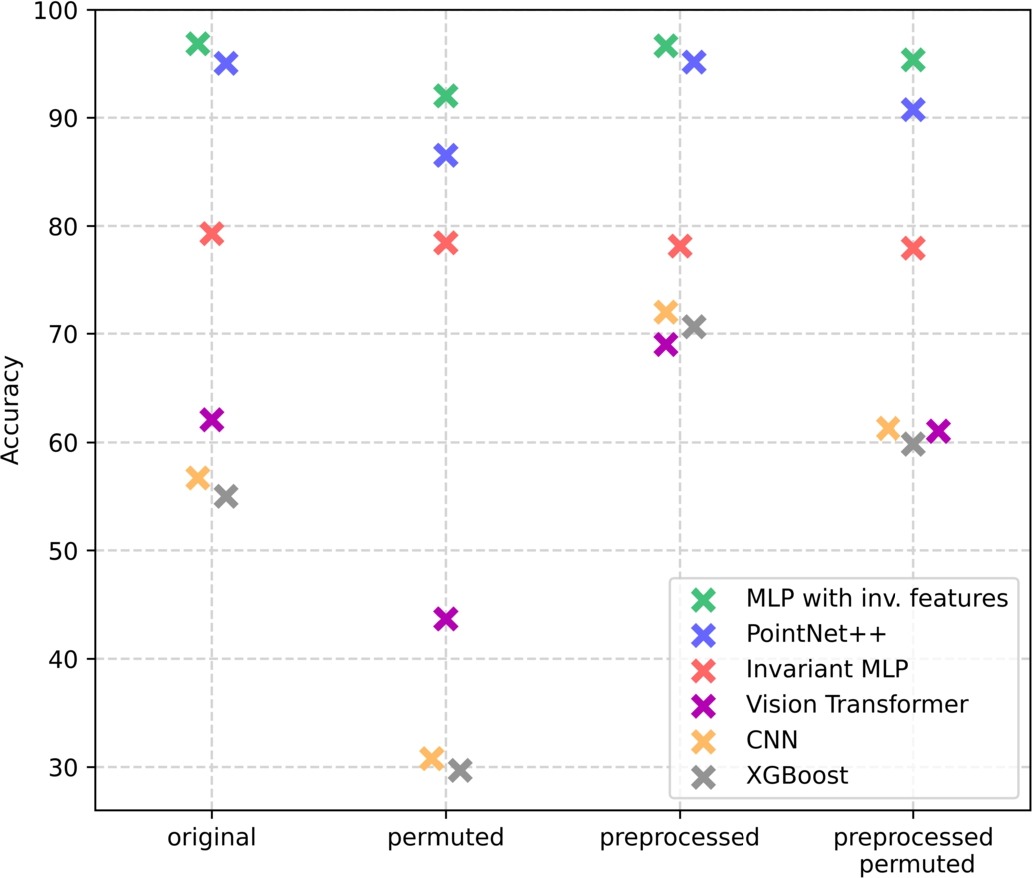
We use supervised machine learning to predict Hodge numbers for Calabi-Yau threefolds encoded by reflexive polyhedra. The Hodge number is invariant to the order of the vertices and the swapping of axes. Incorporating these properties, i.e. the invariance of column and row permutations for a matrix containing the polyhedron’s vertices, promises better performance for Hodge number prediction. On a medium-sized subset of the Kreuzer-Skarke dataset, we train and evaluate approaches with different degrees of invariance. Our comparison shows that machine learning models incorporating symmetries actually outperform models that do not, with our best model achieving almost 97% accuracy.